My first Open Source Contribution in C++ - EVMOne

Recently, I decided to learn the C++ programming language. After a few weeks of study, I felt the need to get hands-on experience with professional code by contributing to open source projects. In this article, I’ll walk you through my very first contribution to an open source project: EVMOne.

EVMOne is an Ethereum Virtual Machine (EVM) implementation written in C++. It can be used as an execution module within other Ethereum clients such as Geth. One of the key advantages of EVMOne is its use of C++, a language well-known for its excellent runtime performance. Theoretically, assuming equivalent implementation, EVMOne should offer the best execution performance among EVMs.

Note: I originally planned to wait until my pull request was merged before publishing this article, but as the review is taking longer than expected, I’ve decided to share my experience now.

The Issue

To get started with the project, I selected a GitHub issue proposed by the core maintainers: Issue #869 – Implement Fast CIOS for Montgomery Modular Multiplication. Before diving into the implementation, I took time to understand what Montgomery modular multiplication is.

Montgomery Modular Multiplication

Montgomery modular multiplication is an efficient method for computing 𝑎⋅𝑏 mod 𝑁 without explicitly performing expensive division operations. Introduced by Peter Montgomery in 1985, it is especially useful in cryptographic algorithms like RSA and elliptic curve cryptography, where many modular multiplications must be performed rapidly.

Instead of working directly with standard modular arithmetic, Montgomery's method transforms numbers into a special form called Montgomery representation, defined as:

𝑎~ = 𝑎⋅𝑅 mod 𝑁

where 𝑅 is a power of 2 greater than 𝑁, usually chosen as 𝑅=2^𝑘 for some integer 𝑘, so arithmetic modulo 𝑅 becomes simple bit masking.

The Montgomery product of 𝑎~ and 𝑏~ is computed as:

Mont(𝑎~, 𝑏~) = 𝑎~ ⋅ 𝑏~ ⋅ 𝑅^(-1) mod 𝑁

This yields a result still in Montgomery form. To convert back to the standard representation, a final Montgomery multiplication with 1 is performed.

The advantage is that division by 𝑁 is avoided. Instead, the method relies on a series of additions, multiplications, and bit shifts, which are much faster on modern hardware. The “CIOS” (Coarsely Integrated Operand Scanning) method is a particular way of organizing the loop structure of the multiplication to balance performance and code simplicity.

Fast CIOS Optimization

In 2022, the paper EdMSM: Multi-Scalar Multiplication for SNARKs and Faster Montgomery Multiplication by Gautam Botrel and Youssef El Housni introduced a way to optimize the CIOS variant of the Montgomery modular multiplication algorithm. The paper showed that if the most significant bit of the word used in intermediate operations is not required (meaning that all variables stay below word_size - 1), then it’s possible to skip some operations, leading to faster average execution.

This assumption often holds true in practice, making this optimization a worthwhile improvement in many cases.

Implementation

The process of resolving the issue involved several steps. The first was to understand the structure and conventions of the EVMOne codebase, and to ensure that I could compile and run the project locally.

Build process for EVMOne.

Once everything was working and all tests passed, I focused on the core of the contribution: the Montgomery algorithm. To fully grasp the optimization, I read several academic papers that detailed the various implementation strategies and explained why the CIOS variant has the lowest computational complexity.

Different variants of the Montgomery algorithm. Source: High-Speed Algorithms & Architectures For Number-Theoretic Cryptosystems by Tolga Acar.

Next, I located the existing Montgomery implementation within EVMOne and compared it with the optimized CIOS variant described in the research paper.

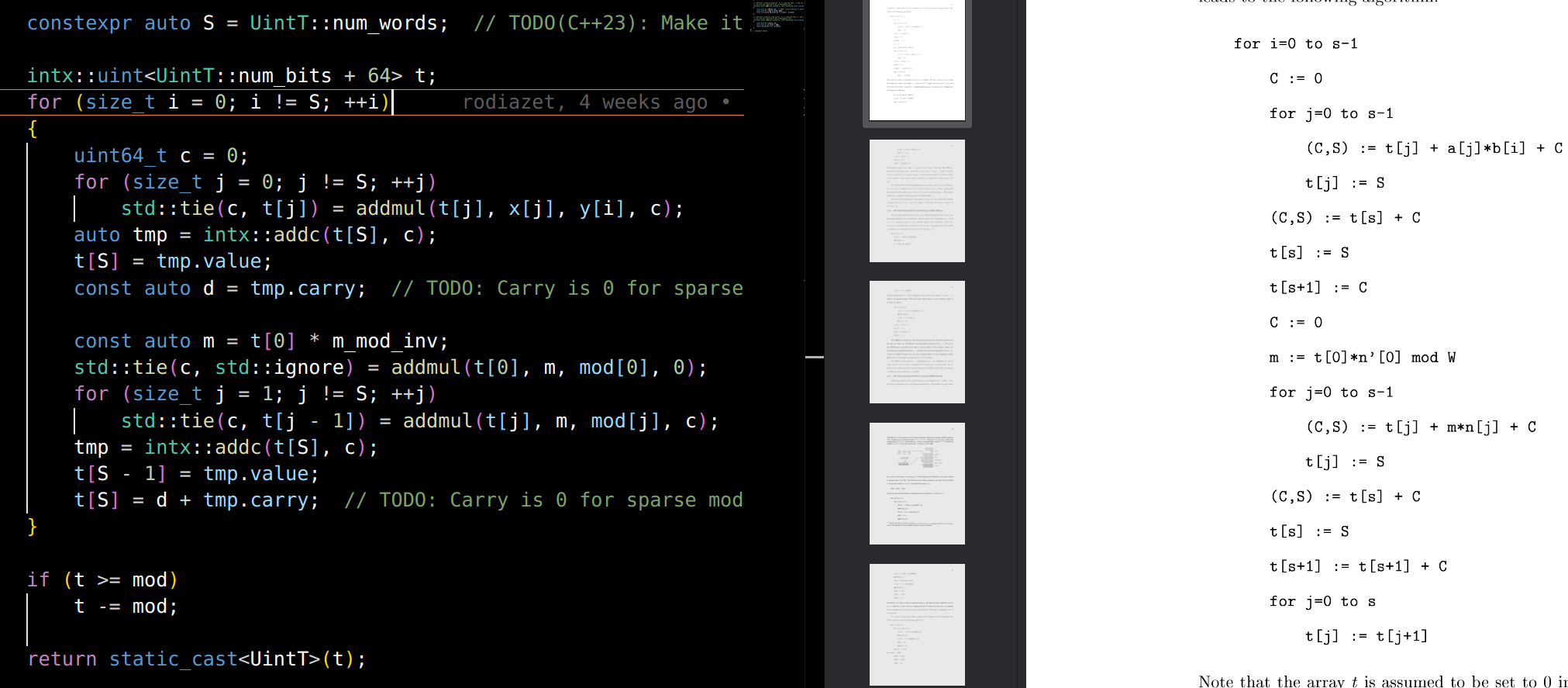
Comparison of the Montgomery implementation in EVMOne with the optimized CIOS variant pseudocode (from EdMSM: Multi-Scalar Multiplication for SNARKs and Faster Montgomery Multiplication).

Finally, I made the necessary code changes to align the implementation with the fast CIOS variant described in the paper:

/// Performs a Montgomery modular multiplication.
constexpr UintT mul(const UintT& x, const UintT& y) const noexcept
{
    constexpr uint64_t most_significant_mod_word_limit{
        std::numeric_limits<uint64_t>::max() >> 1};
    constexpr auto S = UintT::num_words;  
    intx::uint<UintT::num_bits + 64> t;
    for (size_t i = 0; i != S; ++i)
    {
        uint64_t c = 0;
        for (size_t j = 0; j != S; ++j)
            std::tie(c, t[j]) = addmul(t[j], x[j], y[i], c);
   
        uint64_t carry = 0;
        if (mod[S - 1] < most_significant_mod_word_limit)
        { // New branch for Fast CIOS
            carry = c;
        }
        else
        { 
            auto tmp = intx::addc(t[S], c);
            t[S] = tmp.value;
            carry = tmp.carry;
        }
        const auto m = t[0] * m_mod_inv;
        std::tie(c, std::ignore) = addmul(t[0], m, mod[0], 0);
        for (size_t j = 1; j != S; ++j)
            std::tie(c, t[j - 1]) = addmul(t[j], m, mod[j], c);

        uint64_t carry = 0;
        if (mod[S - 1] < most_significant_mod_word_limit)
        { // New branch for Fast CIOS
            t[S - 1] = carry + c;
        }
        else
        {
            auto tmp = intx::addc(t[S], c);
            t[S - 1] = tmp.value;
            t[S] = carry + tmp.carry;
        }
    }
    if (t >= mod)
        t -= mod;
    return static_cast<UintT>(t);
}

As you can see, the modifications are relatively minor, consisting mostly of conditional branches that help eliminate unnecessary operations.

⚠️ Please note: these changes have not yet been reviewed and may contain errors.

After a few trials, all unit tests passed, and I was able to run benchmarks on my own machine to evaluate the performance impact.

Comparing cios_classic.json to cios_improved.json
Benchmark                                               Time             CPU      Time Old      Time New       CPU Old       CPU New
evmmax_mul<uint256, bn254>_median                    -0.1529         -0.1529            27            23            27            23
evmmax_mul<uint256, secp256k1>_median                +0.0059         +0.0058            28            28            28            28

The results showed a consistent 15% performance improvement on the bn254 test cases, which aligns with the expectations set by the research. In my most recent comment on the pull request, I mentioned being unsure why two conditional branches performed better than one. Upon further reflection, I believe this may be due to the use of constexpr, which allows the compiler to eliminate unused branches at compile-time. Having only one conditional branch introduce more instructions and might prevent such optimizations.

You can find the pull request here.

Conclusion

As of writing this article, my pull request has not yet been reviewed. Even though the code changes are minimal and early benchmarks support the claims made in the paper, I can’t be fully certain that the proposed implementation will be accepted.

This experience has been extremely valuable — it taught me more about the mathematical tools involved in elliptic curve cryptography and the implementation of the Montgomery algorithm in high-performance environments.

I hope this article helped you learn something new as well, and that you enjoyed reading it. See you next time!