Opal - Technical Overview

In this article, I’ll dive into the technical underpinnings of the Opal protocol, a project I’ve contributed to extensively. If you haven’t yet read the previous article about Opal, I recommend starting there to better understand the context of what follows.

Here, we’ll focus on two of the protocol’s most important smart contracts: the Omnipool and the Reward Manager.

The Omnipool is the core of the protocol—it’s a single-asset liquidity pool that can dynamically rebalance and reallocate funds across different strategies. It lies at the heart of Opal’s yield-generation mechanism and represents the foundation of the platform's financial logic.

The second contract, the Reward Manager, is one I developed almost entirely independently. Its role is to handle the distribution of rewards to users participating in the Omnipool. I find the mathematical model behind it particularly elegant and effective. While similar systems are likely common and well-studied in DeFi, in this article, we’ll take a closer look at Opal’s unique implementation.

Protocol Overview

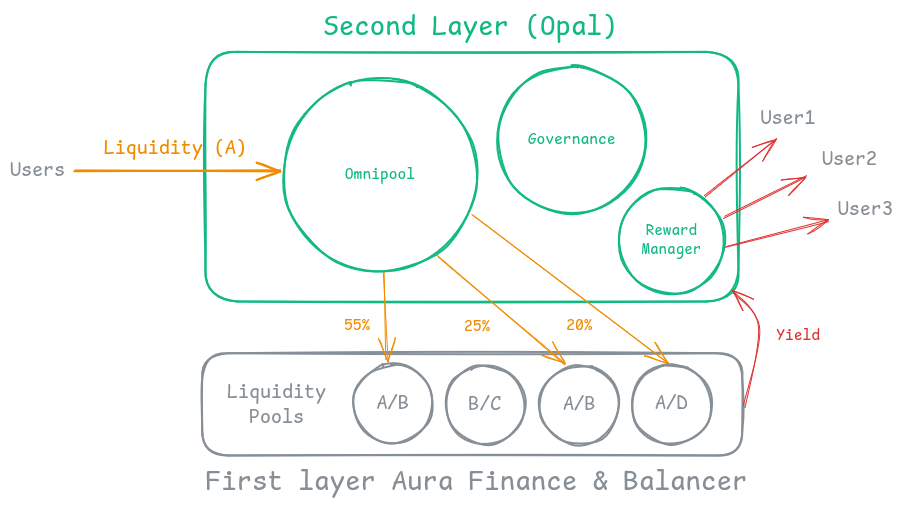
This diagram is a simplified version of the Opal protocol, highlighting the flow of liquidity and rewards managed by the protocol.

The typical operation of an omnipool is as follows:

• For an omnipool that accepts an underlying asset A, the governance module proposes a set of pools along with a distribution weight for the liquidity.
• Liquidity deposited into the omnipool is allocated according to these weights.
• If the current underlying pool weights deviate from those voted by the governance module, an incentive in GEM (the governance token) is distributed to reward rebalancing. The pool weights represents the relative share of the liquidity allocated to each underlying pool.
• Over time, the omnipool accrues rewards, which are tracked by the Reward Manager.
• When a user withdraws their liquidity or chooses to claim their rewards, the Reward Manager distributes the appropriate amount.

The Omnipool

Let’s start by examining the main method of the omnipool: the deposit method.

As a general note for this article: in all code snippets, I systematically remove uninteresting sections such as parameter validation to improve readability.

function depositFor(uint256 _amountIn, address _depositFor, uint256 _minLpReceived) public {
    // Get the price of the underlying asset in USD
    uint256 underlyingPrice = oracle.getUSDPrice(address(underlyingToken));

    // Estimate the value in USD of the liquidity in the omnipool before the deposit
    uint256 beforeTotalUnderlying = _getTotalAndPerPoolUnderlying(underlyingPrice);
    
    // Transfer underlying token to this contract
    underlyingToken.safeTransferFrom(msg.sender, address(this), _amountIn);

    // Estimate the current exchange rate of the omnipool (ie. how much LP tokens are minted for each underlying token deposited)
    uint256 exchangeRate = _exchangeRate(beforeTotalUnderlying);

    // Deposit into Aura Finance (and Balancer V2)
    _depositToAura(beforeTotalUnderlying, _amountIn);

    // Estimate the new value of the liquidity in the omnipool after the deposit
    uint256 afterTotalUnderlying = _getTotalAndPerPoolUnderlying(underlyingPrice);

    // Calculate the increase in the value of the liquidity in the omnipool
    uint256 underlyingBalanceIncrease = afterTotalUnderlying - beforeTotalUnderlying;

    // Calculate the amount of LP tokens that can be minted
    uint256 mintableUnderlyingAmount = _min(_amountIn, underlyingBalanceIncrease);
    uint256 lpReceived = mintableUnderlyingAmount.divDown(exchangeRate);

    // Slippage protection
    if (lpReceived < _minLpReceived) {
        revert TooMuchSlippage();
    }
    lpToken.mint(_depositFor, lpReceived, _depositFor);

    // Handle rebalancing rewards
    _handleRebalancingRewards(...);

    // Emit an event to notify the outside world
    emit Deposit(_depositFor, _amountIn, lpReceived);
}

You'll immediately notice a key feature of contracts dealing with omnipools: everything is denominated in USD, thanks to oracles. Indeed, to maintain a fair balance across multiple underlying pools, it's absolutely essential to accurately price the current value of all positions held by the omnipool.

Opal relies heavily on oracle usage. Every token in every underlying pool must have a reliable price oracle.

This introduces a natural limitation: it's not possible to farm liquidity pools with low market cap tokens, as they often lack trustworthy oracles. Generally, these tokens offer higher APRs because they carry more risk. It's unfortunate to miss out on such opportunities, but this restriction is necessary to ensure the protocol’s overall security.

To conclude on the oracle topic, note that Opal is restricted to use Chainlink and Redstone feeds. These lists define the full range of tokens eligible for integration into new underlying pools.

To estimate the value of a position held by the omnipool, we rely on:

• the USD price of each token forming the underlying Balancer pool, and
• the math provided in the Balancer documentation, which governs pool behavior.

This document provides a detailed explanation of the math used to estimate the value of a Balancer Pool Token (BPT).

As for the rest, I won’t go deeper into the omnipool methods in this article. However, if you're interested in exploring the full implementation, the smart contract code is publicly available on Etherscan.

The Reward Manager

Let’s now discuss the Reward Manager — a key module responsible for distributing rewards to users.

More specifically, the rewards accumulated by the omnipool are distributed by Balancer and Aura Finance in the form of their respective governance tokens: BAL and AURA.

In some cases, external protocols may incentivize users to provide liquidity by offering extra rewards. These are one-off or special tokens distributed in addition to BAL and AURA. For simplicity, the following examples focus only on handling BAL tokens, but the logic can be duplicated to support any other reward token.

It’s also worth noting a crucial difference from Uniswap: In Uniswap, a liquidity pool A/B typically distributes claimable rewards in both token A and B. In Balancer V2, however, profits are directly reinvested into the BPT (Balancer Pool Tokens), increasing their intrinsic value.

This means there’s no need to redistribute LP token rewards — only the reward tokens emitted by the underlying protocols integrated into Opal.

Modeling and Distributing Rewards

Before diving into the code, let’s break down the mathematical model behind reward accumulation and distribution.

To accurately track the rewards accrued by the omnipool over time, we use a mathematical integral — denoted as R (for Rewards). An integral is monotonic and non-decreasing, which perfectly matches our use case:

The omnipool can only accumulate rewards over time, never lose them.

To be more precise, R expresses the values of one unit of LP token in the omnipool over time.

As a simplified example, imagine a linear curve representing R over time — a case where the omnipool receives a constant flow of rewards and is updated at each block:

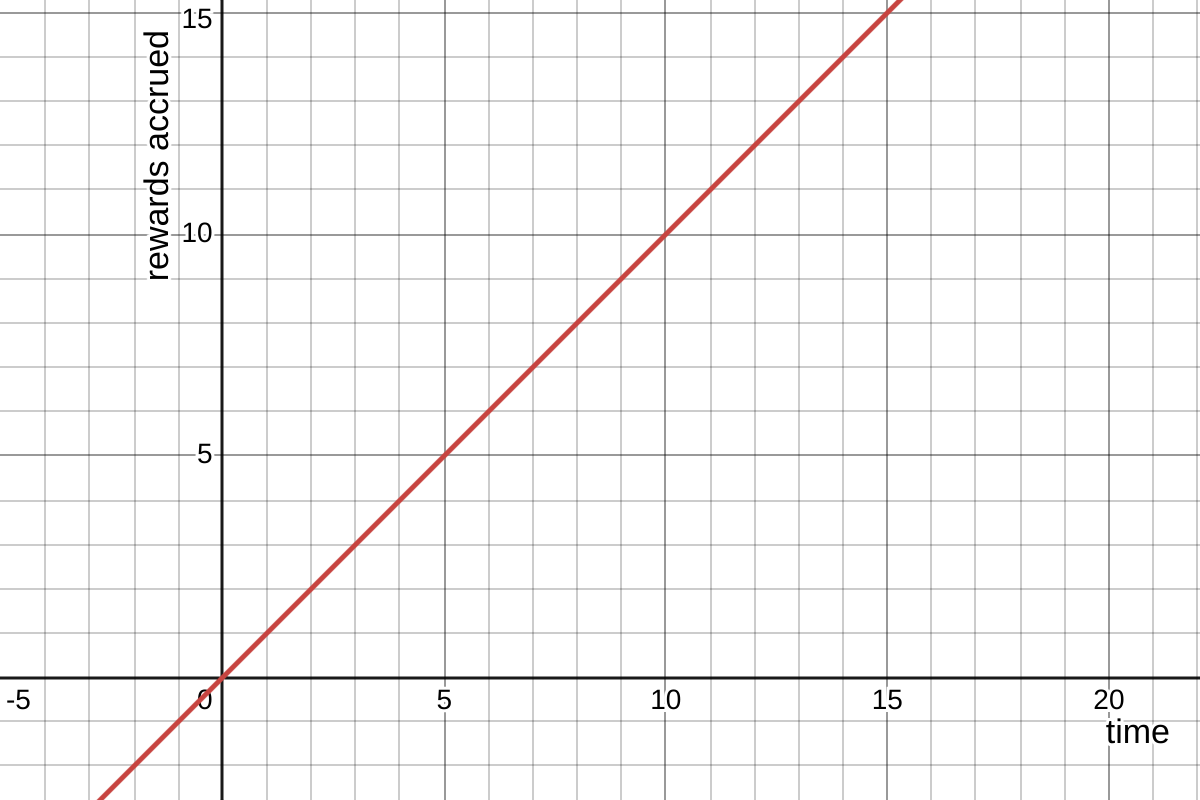
R(t) = constant × t (very simple case). Source Desmos.

When a user joins the omnipool, we need to store the value R(t) at that moment, representing the accumulated rewards before their participation.

When the user decides to claim their rewards, we simply:

• Retrieve the current reward state R(t+1)
• Subtract the value at their join time R(t)
• Compute the reward delta: reward = R(t+1) - R(t)

This delta is always ≥ 0 and represents the rewards accrue by one unit of the LP token in the omnipool at t+1 minus the value at t.

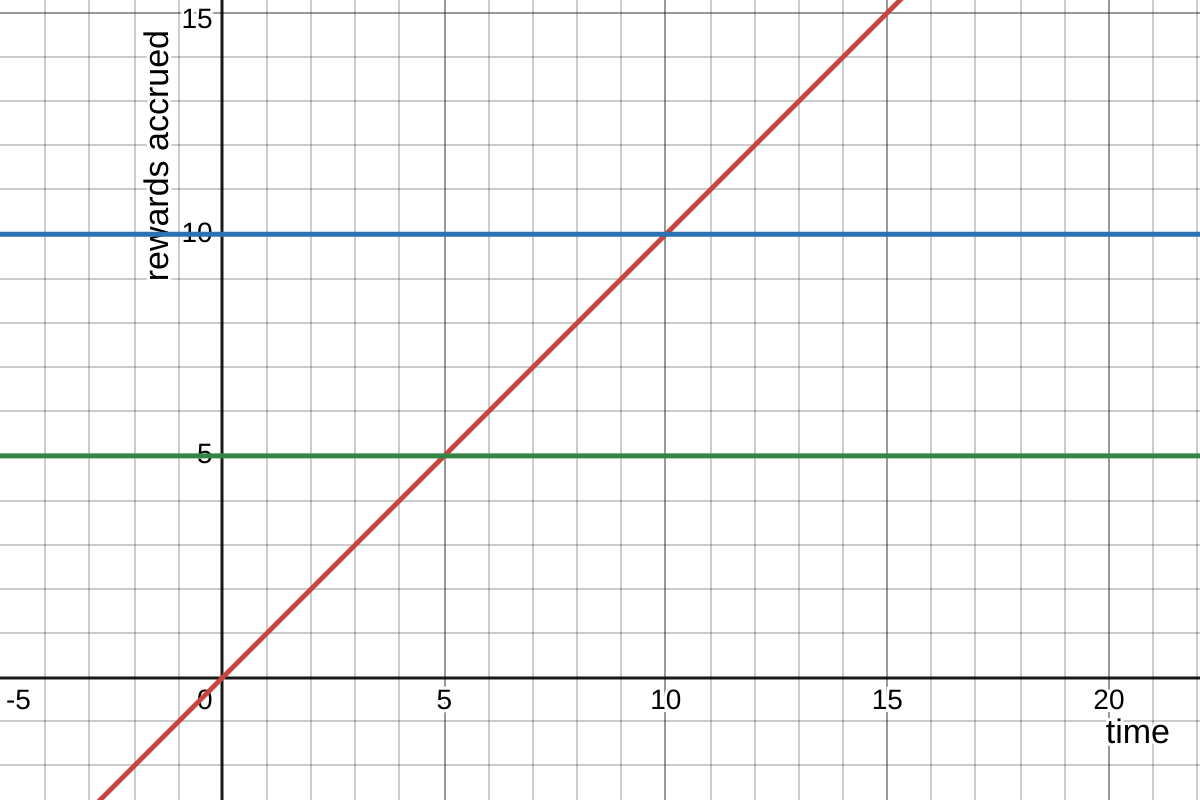
On this diagram, t=5 and t+1=10. The rewards accrued by one unit of the LP token in the omnipool between t and t+1 is R(t+1) - R(t) = 10 - 5 = 5. Source Desmos.

Now, the remaining step is to distribute the rewards among liquidity providers proportionally to their share in the pool. This share is known, as it directly corresponds to their current balance. The final formula is:

reward = balance * (R(t+1) - R(t)) (we don't see totalSupply in the formula because it's contained in R).

Implementation

Now that we have been through the mathematical model, let's take a look at the updateUserState function, which is called whenever a user deposits or claims rewards. It updates both the global omnipool state and the individual user’s reward data:

function updateUserState(address _account) public {
    // Get the user's LP balance
    uint256 deposited = omnipool.balanceOf(_account);

    // Update the pool state, claim rewards, and transfer them to the Reward Manager
    _updateOmnipoolState();

    // Update the user's pending rewards
    _updateRewards(_account, deposited);
}

The logic is straightforward, let's see what's inside of _updateOmnipoolState:

function _updateOmnipoolState() internal {
    // Claim rewards accrued from underlying protocols
    uint256 earnedBAL = _claimOmnipoolRewards();

    // Get the total amount of LP tokens deposited into the omnipool
    uint256 totalDeposited = omnipool.totalSupply();

    // Update the global reward state
    BALMeta.earnedIntegral += (earnedBAL * SCALED_ONE) / totalDeposited;
    BALMeta.lastEarned += earnedBAL;

    // Update the last balance of BAL in the omnipool
    lastBALBalance = IERC20(BAL).balanceOf(address(omnipool));

    // Emit an event to notify the claimed rewards
    emit RewardUpdated(earnedBAL);
}

Here we perform:

• Reward collection via _claimOmnipoolRewards()
• Update of the reward integral (R) for the BAL token. As we can see, BALMeta.earnedIntegral represents the earned BAL rewards devided by the total supply of LP tokens (ie. the reward accrued by one unit of LP token).
• Update of the last balance of BAL in the omnipool

You probably noticed that BALMeta is a struct used to store reward accounting data for a specific token — in this case, BAL. See the full struct below:

struct RewardMeta {
    uint256 earnedIntegral; // a scaled running total of reward per unit of LP token (R)
    uint256 lastEarned; // the last total amount of reward received
    mapping(address => uint256) accountIntegral; // the value of R at the time of the user's last update
    mapping(address => uint256) accountShare; // amount of reward to distribute to the user
}

It stores both global and per-user reward accounting data.

Finally, let's take a look at the _updateRewards function, which updates the user's reward share and integral:

function _updateRewards(address account, uint256 balance) internal {
    // Get the difference between the global and per-user reward integral (ie. R(t+1) - R(t))
    uint256 BALIntegralDelta = BALMeta.earnedIntegral - BALMeta.accountIntegral[account];

    // Calculate the amount of reward to distribute to the user
    uint256 balShare = (balance * BALIntegralDelta) / SCALED_ONE;

    // Update the user's reward share
    BALMeta.accountShare[account] += balShare;

    // Update the user's reward integral
    BALMeta.accountIntegral[account] = BALMeta.earnedIntegral;

    // Emit an event to notify the claimed rewards
    emit RewardUpdated(account, BALIntegralDelta);
}

This logic ensures:

• Users only earn rewards for periods where they were actively staked
• The reward share is fairly proportional to their balance and holding duration

The final piece of the puzzle is the claimEarnings function. It updates the state of the omnipool and the user, then transfers the accrued rewards to the user's address.

function claimEarnings() external {
    // Update the user's reward state
    updateUserState(msg.sender);

    // Get the share amounts and reset them to 0
    uint256 balAmount = BALMeta.accountShare[msg.sender];
    BALMeta.accountShare[msg.sender] = 0;

    // Transfer the rewards to the user
    BALToken.safeTransferFrom(address(this), msg.sender, balAmount);
    lastBALBalance = IERC20(BAL).balanceOf(address(this));

    emit RewardClaimed(msg.sender, balAmount);
}

You can find the full implementation of the Reward Manager here.

Toward a More Concrete Example

Now that you've seen the mathematical model and its implementation, I just wanted to show you a more realistic example to keep in mind.

In the graph below, we represent the evolution of R(t). As you can see, the progression takes the form of a step function. This is because the accrued rewards are only updated from the Reward Manager’s perspective when the corresponding functions are called.

Additionally, the evolution of R(t) is not linear. It depends on both the liquidity of the omnipool and the APRs of the underlying pools that compose it.

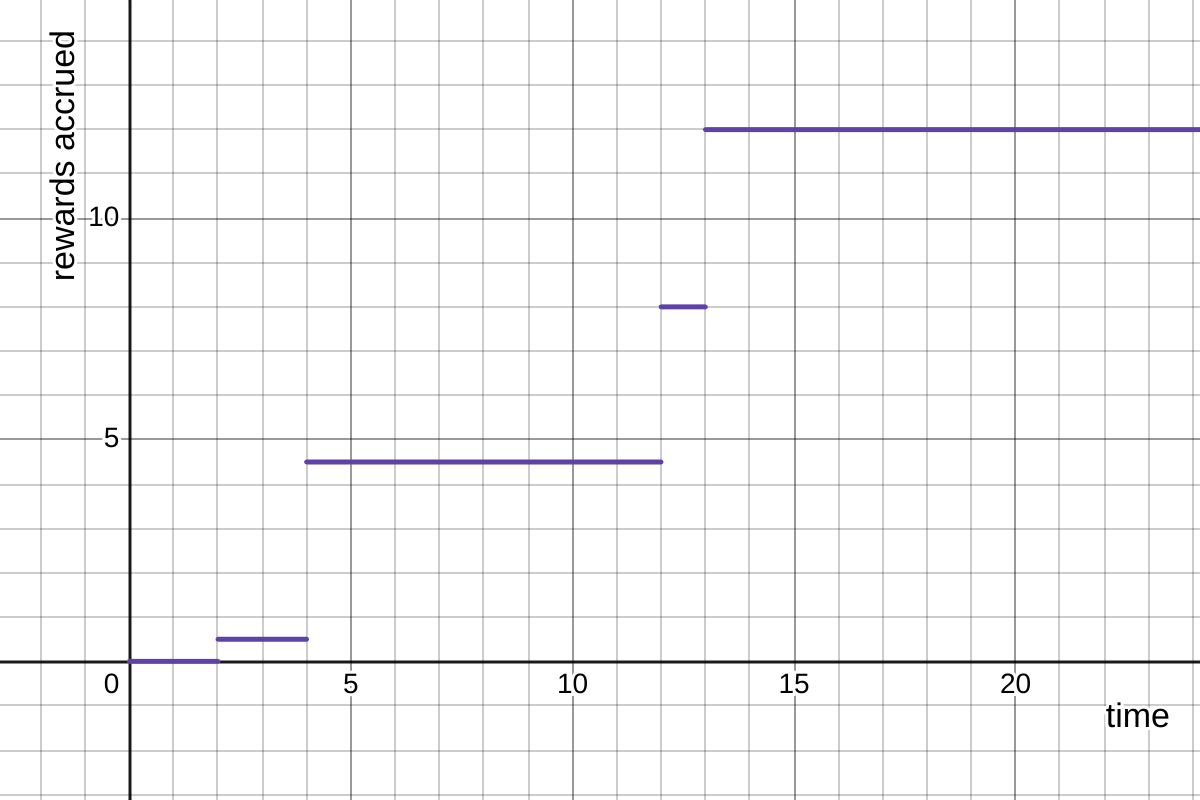
R(t) more realistic evolution. Source Desmos.

Conclusion

Let's wrap up this article on the inner workings of the Omnipool and the Reward Manager. I hope it helped you gain a better understanding of the Opal protocol and introduced you to some interesting mechanisms you might consider for your own future work. There are other noteworthy components we haven’t covered here, such as the governance module and the rebalancing system—areas I’ve been less involved with. But perhaps that’ll be a good reason to write a second article. See you soon!